Unsatisfied with my last investigation into dependency breaking I decided to dig a little deeper.

First, instead of using hyperfine I’ve used Daniel Lemire’s (an absolute SIMD beast by the way, highly recommend reading his blog and marveling at simdjson) benchmarking harness and instead of a shared CPU I’ve used a dedicated host. I’ve also used C++ with -O1, which generates basically the same code as my handwritten assembly, but is much easier to work with.

As a refresher, we had two implementations of sum, one I expected to be slower

int result = 0;

for (int i = 0; i <= N/2; i++) {
    result += arr[2*i];
    result += arr[2*i+1];
}

return result;

And one I expected to be faster, thanks to the two operations in the loop being independent of each other, allowing out-of-order execution:

int result1 = 0;
int result2 = 0;

for (int i = 0; i <= N/2; i++) {
    result1 += arr[2*i];
    result2 += arr[2*i+1];
}

return result1 + result2;

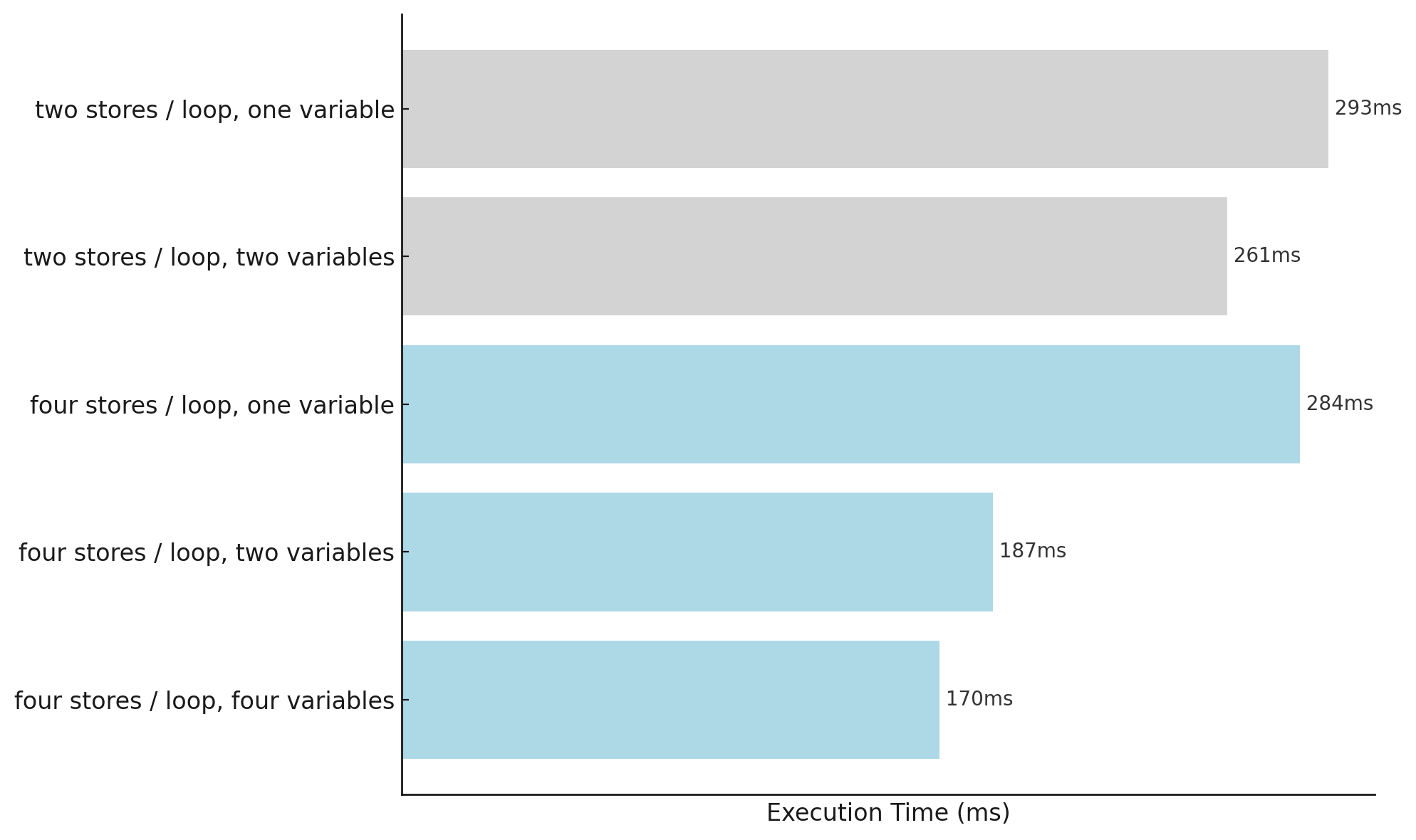
With hyperfine on a shared CPU it was impossible to distinguish which is which. With perf events, I’m able to measure a consistent difference: the single variable implementation finishes in 293ms and the two variable in 261ms, ie. about 12% faster.

What’s more interesting though, is what happens when I unroll the loop even more and use 1, 2 or 4 variables:

int result1 = 0;
int result2 = 0;
int result3 = 0;
int result4 = 0;

for (int i = 0; i <= N/4; i++) {
    result1 += arr[2*i];
    result2 += arr[2*i+1];
    result3 += arr[2*i+2];
    result4 += arr[2*i+3];
}

return result1 + result2 + result3 + result4;

The one variable version gets slightly faster at 284ms, presumably due to lower loop overhead, but the 2 and 4 variable version speed up considerably more to 187ms and 170ms respectively, ie. 35% faster!

graph

Unsurprisingly these differences disappear when I use -O3.

Pretty cool! Wish I had a more precise understanding of why this happen though.